Shortcuts

Title Page

Recovering Missing Coefficients in DCT-Transformed Images

Shujun Li¹, Andreas Karrenbauer¹, Dietmar Saupe¹ and C.-C. Jay Kuo<sup>2

1</sup> University of Konstanz, Germany
² University of Southern California, USA

In Proceedings of 2011 18th IEEE International Conference on Image Processing (ICIP 2011, Brussels, Belgium, September 11-14, 2011), pp. 1569-1572, 2011.

Copyright 2011 IEEE. Published in the 2011 IEEE International Conference on Image Processing (ICIP 2011), September 11-14, 2011, Brussels, Belgium. Personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works, must be obtained from the IEEE. Contact: Manager, Copyrights and Permissions / IEEE Service Center / 445 Hoes Lane / P.O. Box 1331 / Piscataway, NJ 08855-1331, USA. Telephone: + Intl. 908-562-3966.

Abstract

A general method for recovering missing DCT coefficients in DCT-transformed images is presented in this work. We model the DCT coefficients recovery problem as an optimization problem and recover all missing DCT coefficients via linear programming. The visual quality of the recovered image gradually decreases as the number of missing DCT coefficients increases. For some images, the quality is surprisingly good even when more than 10 most significant DCT coefficients are missing. When only the DC coefficient is missing, the proposed algorithm outperforms existing methods according to experimental results conducted on 200 test images. The proposed recovery method can be used for cryptanalysis of DCT based selective encryption schemes and other applications.

Links

• The paper: Papers/ICIP2011.pdf
• The Poster: Papers/ICIP2011-Poster.pdf
• BibTEX: Papers/ICIP2011.txt

• Database (198 images): Papers/Data/ICIP2011/Images.zip (15 MB)
  • 98 test images collected from the different standard test image databases plus two images taken by Shujun Li (we do NOT hold the copyrights except for Japanese_Harpists.pgm and Pipa_Player.pgm whose copyrights are held by Shujun Li).
  • 98 images taken by Shujun Li from 2003-2008. (Update on 23 August 2021: The original release included 100 images, but two were removed because of some legal considerations.)
  • All images whose copyrights are held by Shuju Li are released under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License .
    You are appreciated if you can inform Shujun Li for using this database for your own research.
• Source code: Papers/Data/ICIP2011/source_code_Cplex_Class.zip (a simpler version based on CPLEX MATLAB class; for other implementations please contact Shujun)

• Question: What is the difference between the 200 test images and those used in your ICIP2010 paper [2]?
• Answer: They are the same images. Actually the 200 test images above are rescaled editions of those used in our ICIP2010 paper. The reason why we didn't use the 200 images of the original size is that the optimization algorithm becomes relatively slow when handling e.g. 512x512 images. How to handle large images effectively is one of the future research topics as we pointed out in our paper.

External links

• MeTriX MuX Visual Quality Assessment Package: http://foulard.ece.cornell.edu/gaubatz/metrix_mux

Previous Methods

Previous methods can only recover DC coefficients from AC ones. There are only two known methods, which are both based on local propagation and the following two properties.

• Property 1: The difference between two neighboring pixels is a Laplacian variate with zero mean and a small variance.
• Property 2: The range of pixel values calculated from DC-free edition of a block (i.e., only from AC coefficients of this block) constrains the value of the DC coefficient of this block.

In the following, we will only show how different the results of the two methods are. To get more ideas about the two methods, please click here.

USO

• USO = Uehara, Safavi-Naini and Ogunbona (authors of [1])

FRM

• FRM = Under/Over-Flow Rate Minimization (FRM) [2]

Our Optimization Model

FRM is still not good enough!

We need global optimization!

The recovery problem of any missing DCT coefficients from known ones can be modeled as a linear program, thus allowing global optimization towards an objective.

• Unknowns and Knowns:
  • Pixel values (Unknowns): X(i,j)
  • DCT coefficients (Variable): Y(i,j)
  • DCT coefficients (Knowns): Y*(i,j)
• Objective: minimize total variation = Σ{all adjacent pixel pairs (X(i,j),X(i',j'))}|X(i,j)-X(i',j')|
• Constraints:
  • Y = A * X
  • X_min ≤ X(i,j) ≤ X_max
  • Y(i,j) = Y*(i,j) for known DCT coefficients

Experimental Results

AC2DC

We also compared the linear program based approach with FRM, and found out that the former achieves an overall better performance as expected. In the following figure, we show the difference between the visual quality of the images recoverd via linear program and that via FRM. A positive value suggests that the linear program based approach is better. The red lines show the average difference over all the 200 test images.

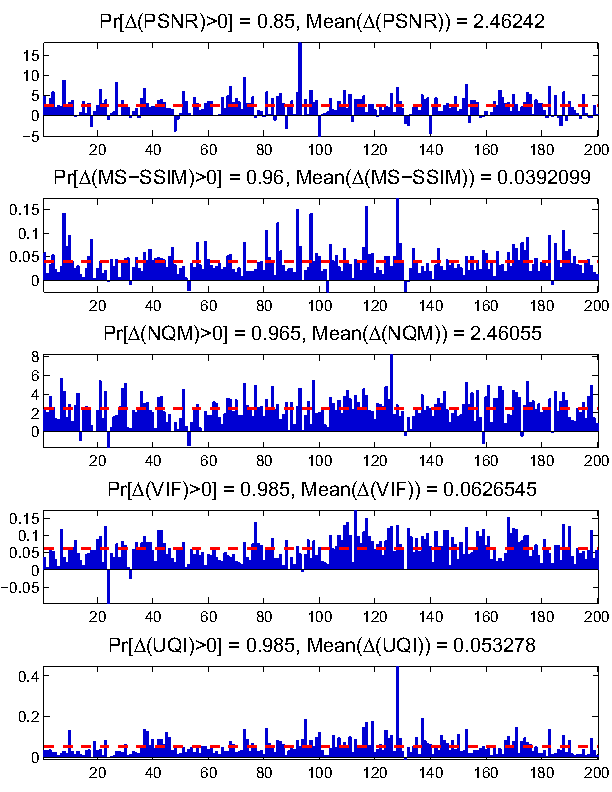
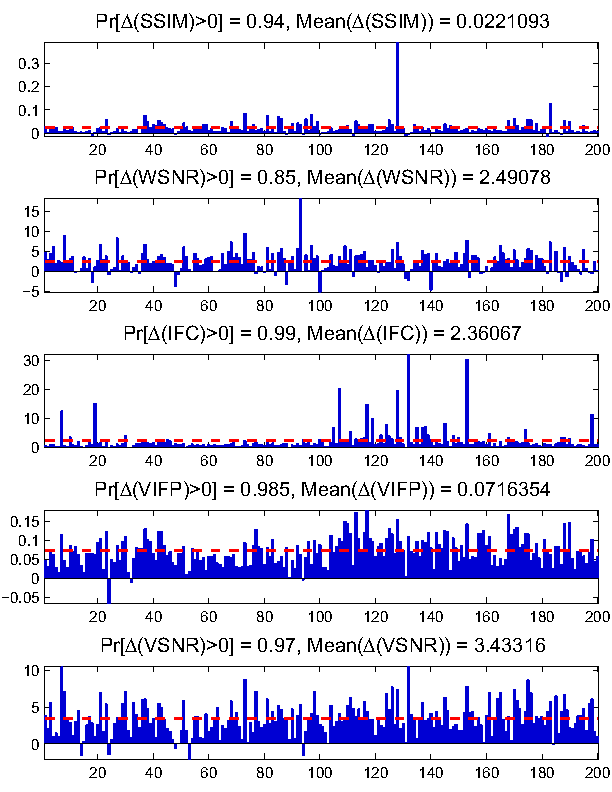
DCT2DCT

↓

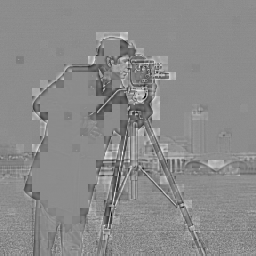
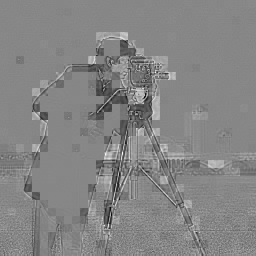
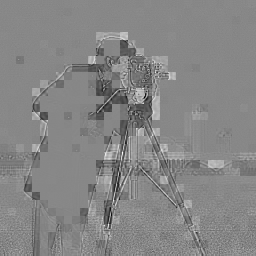
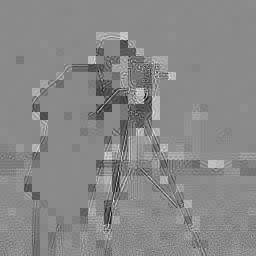
Key References

[1]  Takeyuki Uehara, Reihaneh Safavi-Naini, and Philip Ogunbona, "Recovering DC coefficients in block-based DCT," IEEE Transactions on Image Processing, vol. 15, no. 11, pp. 3592-3596, IEEE, 2006

[2]  Shujun Li, Junaid Jameel Ahmad, Dietmar Saupe and C.-C. Jay Kuo, "An Improved DC Recovery Method from AC Coefficients of DCT-Transformed Images," In Proceedings of 17th IEEE International Conference on Image Processing (ICIP 2010, Hong Kong, China, September 26-29, 2010), pp. 2085-2088, IEEE, 2010 Companion Web Page